若干定义
基本设定
分别给定一个hospitals对students的偏好集合,和一个students对hospitals的偏好集合,对hospitals和students进行一一配对。
unstable pair
如果存在这样一个hospital(h)和student(s)对,同时满足以下两点:
- 相比现在分配到的student,h更偏好s
- 相比现在分配到的hospital,s更偏好h
则称h-s是unstable pair。
即unstable pair一定是现在的matching中不存在的pair。
stable assignment
不存在unstable pair的分配策略,称为stable assignment或stable matching。
例子
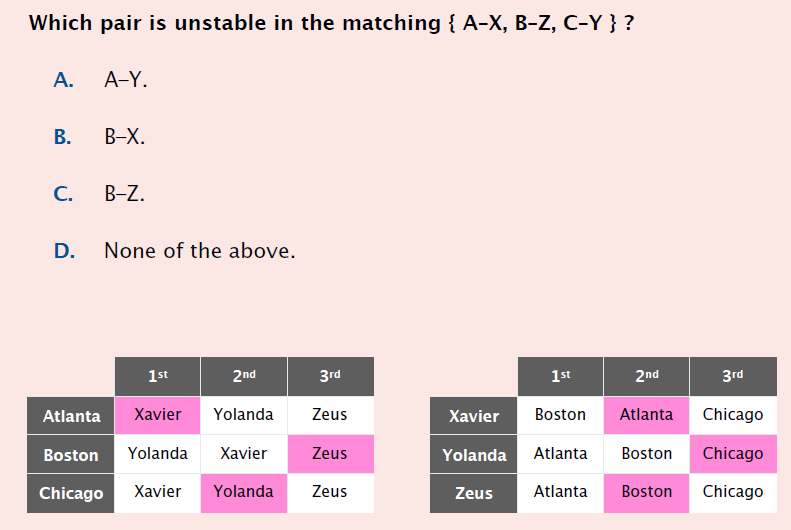
B选项中的pair B-X,即是一个unstable pair。
因为在当前的匹配中,相比已经分配到的Z,B更偏好X;而相比已经分配到的A,X更偏好B,故满足上述定义。
Gale-Shapley 算法
首先要说明,stable matching并不总是存在的。
上述说法存疑
算法步骤
Gale-Shapley算法用于寻找稳定匹配。依然用hospitals和students的匹配问题为例,算法步骤如下:
INITIALIZE M //M是初始为空的匹配
while(还有hospital没被匹配,且其尚未对每一个student都propose一次)
{
//s是h的偏好列表中第一个还未被propose的student
if(s尚未被匹配) 将h-s添加到M;
else if(相比已经被分配到的h',s更偏好h) 用h-s代替M中已存在的h'-s;
else s拒绝h的propose;
}
RETURN M //此时M为stable matching 证明算法有效性
不难观察到两个事实:
- hospitals按其偏好的降序对students提出propose
- 一旦一个student被匹配成功,他将不会变为失配状态,处境也不会更坏。也就是说,要么维持现状,要么得到一个比现在“更好”的匹配。
不难理解:
- 算法在经过至多 $n^2$ 次
WHILE循环后终止。 - 算法最后总是输出一个匹配。
- 所有hospitals最后都会被成功匹配。(反证法可证)
- 所有students最后都会被成功匹配。(由4可得)
- 在Gale-Shapley算法生成的组合M*中,不存在unstable pairs。
下面证明5的正确性。
我们考虑任何不在M*中的pair h-s,可以将其分为两类:
- h从未propose过s,说明存在一个s',它在h的偏好列表上排在s的前面,所以h-s不会是unstable的。
- h已经propose过s,说明s拒绝了h(立刻或者稍后),故对于s,有一个“更好”的h',所以h-s依然不会是unstable的。
综上,不论哪种情况,都不存在M*外的h-s是unstable的。
Gale-Shapley算法保证对任何实例问题都能找到一个stable matching。
此外,虽然一个实例问题可能会存在若干种不同的stable matching,且此算法是nondeterministic(非确定性)的,以任何顺序执行此算法,都只会得出同一个stable matching。
hospital optimality
当以hospitals为propose的提出方,students为propose的接受方时,算法是倾向对hospitals有利的。
前面提到,对于一个实例问题,可能存在若干不同的stable matching。基于此,我们做如下定义:
Def.如果在任一stable matching中,存在h-s的pair,则称s是h的valid partner。
我们说Gale-Shapley算法是hospital-optimal的,因为在算法结果中,每一个hospital总能匹配到它的best valid partner。
下面对此进行证明。
证明
M*是此算法生成的stable matching
- 我们假设h被s拒绝,是算法执行中发生的第一次hospital被自己的valid partner拒绝的事件。
- 显然存在一个stable matching M,内含h-s这一pair。
- 由于在M*中s拒绝了h,说明存在一个h',满足 s prefers h' to h
- 假设在M中h'的配对student是s'。
- 在M*中,当h被s拒绝时,h'还没有被拒绝过,。也就是说,h'在没有向s'提出过propose的情况下与s配对了。故满足 h' prefers s to s'
现在整理一下。在stable matching M中,存在两个pair:h-s和h'-s'。但是,我们由上述推导得出两个小结论,s prefers h' to h,且h' prefers s to s'。显然,h'-s构成了一个unstable pair,所以M不是一个stable matching。
故得证。
student pessimal
事实上,hospital-optimality是以student的利益为代价的。每一个student在算法结果中都得到了worst valid partner。
下面对此进行证明。
证明
- 假设在M*中,h-s为一个pair,且h不是s的worst valid partner。也就是说,存在一个比h“更坏”的h'。s prefers h to h'
- 在一个stable matching M中,存在两个pair,h'-s和h-s'。
- 基于已经证明的hospital-optimality,s是h的best valid partner(因为M*中存在h-s)。即 h prefers s to s'。
显然,在M中,h-s构成了一个unstable pair,故M不是一个stable matching。
故得证。
一点尾巴
在以hospitals为主动的Gale-Shapley算法中,hospitals无法以谎报自己的preference来获得更好的结果。




Comments NOTHING